In this tutorial we will demonstrate how to implement Example 5.1: Blackjack from Reinforcement Learning (Sutton and Barto).
Blackjack is a card game where the goal is to obtain cards the sum of whose values is maximised without exceeding 21. All face cards (Jack, Queen, King) count as 10. An ace counts as 1 or 11 and we shall see below how this is determined.
The example uses first-visit Monte Carlo prediction to estimate the values $v_\pi(s)$ of each state $s$ under policy $\pi$ as the average of the returns following the first visits to $s$.

In code for an arbitrary episode generating function episode_fn
def first_visit_mc_prediction(pi, gamma, states, num_episodes, episode_fn):
num_states = len(states)
V = dict(zip(states, np.random.normal(size=num_states)))
returns = {state: [] for state in states}
for episode in tqdm.trange(num_episodes):
episode = episode_fn(pi)
S_0Tm1, A_0Tm1, R_1T = episode
G = 0
for t, (St, At, Rtp1) in list(enumerate(zip(*episode)))[::-1]:
G = gamma * G + Rtp1
if St not in S_0Tm1[:t]:
returns[St].append(G)
V[St] = np.mean(returns[St])
return V
Now let us implement a function that generates blackjack episodes
import numpy as np
import matplotlib.pyplot as plt
import itertools
from tqdm import autonotebook as tqdm
The game begins with two cards dealt to both dealer and player. One of the dealer’s cards is face up and the other is face down. If the player has 21 immediately (an ace and a 10-card), it is called a natural. He then wins unless the dealer also has a natural, in which case the game is a draw. If the player does not have a natural, then he can request additional cards, one by one (hits), until he either stops (sticks) or exceeds 21 (goes bust). If he goes bust, he loses; if he sticks, then it becomes the dealer’s turn. The dealer hits or sticks according to a fixed strategy without choice: he sticks on any sum of 17 or greater, and hits otherwise. If the dealer goes bust, then the player wins; otherwise, the outcome—win, lose, or draw—is determined by whose final sum is closer to 21.
The state will be as follows
the player makes decisions on the basis of three variables: his current sum (12–21), the dealer’s one showing card (ace–10), and whether or not he holds a usable ace. This makes for a total of 200 states.
Here is how we will interpret and implement the game
-
Initially dealer gets two cards, one face up and another face down. Any subsequent cards given to dealer are face down. The state is
(current_sum_P, D_up, usable_ace_P), whereD_updoes not change whilstcurrent_sum_Pandusable_ace_Pcan change - If player has a “natural”, then dealer does not get to hit and the score of the dealer’s first two cards is used to determine the result
- Both player and dealer always “hit” until their score is at least 12. Only then does the policy kick in. Here is why:
- First we need to mention the idea of a “usable ace”
If the player holds an ace that he could count as 11 without going bust, then the ace is said to be usable. In this case it is always counted as 11 because counting it as 1 would make the sum 11 or less, in which case there is no decision to be made because, obviously, the player should always hit.
- Why? Because to count the ace as 11 without going bust the total so far must be 10 or less which would mean counting the ace as 1 would make the sum 11 or less. Note that there can be at most one usable ace since two or more would lead to a total of 22 or above.
- Whilst the score is less than or equal to 10, since cards have a maximum value of 11, no card can make it more than 21.
- Once the score is 11, provided aces are always counted as 1, no card can make the total more than 21
- It is only after the score is at least 12 that there is a risk of going bust and when a policy is needed.
- For hits after the score is at least 12, if the value of the new card would make the total exceed 21 and a usable ace exists, we will count the ace as 1 instead of 11, subtracting 10 from the score and making the ace no longer usable.
def blackjack_episode(pi):
def initialise(pair):
current_sum = pair.sum()
usable_ace = False
if (pair == 1).any():
current_sum += 10
usable_ace = True
# While < 11, ace is usable
while current_sum < 11:
deal = np.random.choice(cards)
current_sum += deal
if deal == 1:
current_sum += 10
usable_ace = True
# Since < 12, won't go bust adding any card (ace counted as 1)
# since max card value is <= 10
if current_sum == 11:
current_sum += np.random.choice(cards)
return current_sum, usable_ace
def hit(current_sum, usable_ace):
current_sum += np.random.choice(cards)
if current_sum > 21 and usable_ace:
current_sum -= 10
usable_ace = False
return current_sum, usable_ace
states = []
actions = []
rewards = []
cards = np.minimum(np.arange(1, 14), 10)
D_up, D_down = cards_D = np.random.choice(cards, size=2)
cards_P = np.random.choice(cards, size=2)
if set(cards_P) == {1, 10}:
states.append((21, D_up, True)) # natural
actions.append('stick')
if set(cards_D) == {1, 10}:
rewards.append(0)
else:
rewards.append(1)
return states, actions, rewards
current_sum_P, usable_ace_P = initialise(cards_P)
states.append(
(current_sum_P, D_up, usable_ace_P)
)
while True:
current_sum_P, _, usable_ace_P = state = states[-1]
action = pi(state)
actions.append(action)
if action == 'hit':
current_sum_P, usable_ace_P = hit(current_sum_P, usable_ace_P)
if current_sum_P > 21:
rewards.append(-1)
break
else:
rewards.append(0)
states.append((current_sum_P, D_up, usable_ace_P))
else:
# Dealer's turn
current_sum_D, usable_ace_D = initialise(cards_D)
while current_sum_D < 17:
current_sum_D, usable_ace_D = hit(current_sum_D, usable_ace_D)
if current_sum_D > 21:
rewards.append(1)
elif current_sum_D > current_sum_P:
rewards.append(-1)
elif current_sum_D == current_sum_P:
rewards.append(0)
else:
assert current_sum_D < current_sum_P
rewards.append(1)
break
return states, actions, rewards
Consider the policy that sticks if the player’s sum is 20 or 21, and otherwise hits.
def default_policy(state):
total, *_ = state
if total < 20:
return 'hit'
return 'stick'
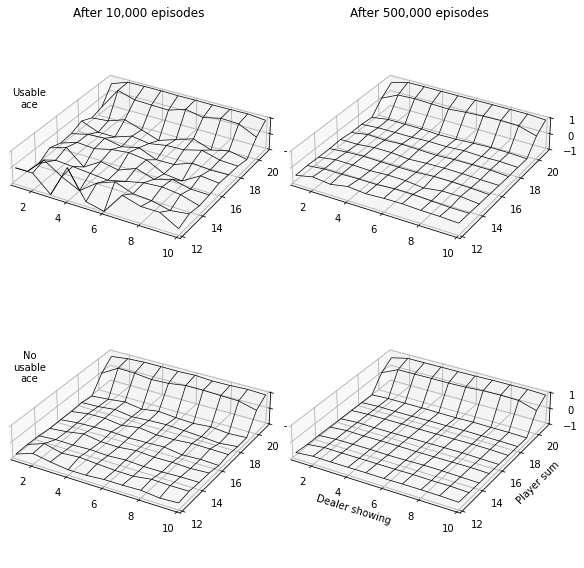
Let us now plot a figure similar to Figure 5.1 in the book. First we need to run first_visit_mc_prediction for 10k and 500k episodes.
_pi = default_policy
_gamma = 1
_showing_card = range(1, 11)
_current_sum = range(12, 22)
_usable_ace = [True, False]
_states = list(itertools.product(_current_sum, _showing_card, _usable_ace))
print('Number of states:', len(_states))
value = dict()
for _num_episodes in [10, 500]:
_episode_fn = blackjack_episode
print(f'Number of episodes: {_num_episodes},000')
value[_num_episodes] = first_visit_mc_prediction(
_pi, _gamma, _states, _num_episodes * 1000, _episode_fn)
Number of states: 200
Number of episodes: 10,000
0%| | 0/10000 [00:00<?, ?it/s]
Number of episodes: 500,000
0%| | 0/500000 [00:00<?, ?it/s]
fig = plt.figure(figsize=(8, 8))
for idx, (ne, val) in enumerate(value.items(), 1):
for i, u_ace in zip(range(0, 3, 2), [True, False]):
axis = fig.add_subplot(2, 2, idx + i, projection='3d')
if i == 0:
axis.set_title(f'After {ne},000 episodes')
X, Y = np.meshgrid(_showing_card, _current_sum)
Z = np.zeros_like(X).astype('float')
for (cs, sc, ua), v in val.items():
if ua == u_ace:
Z[cs-12, sc-1] = v
axis.plot_wireframe(X, Y, Z, linewidth=0.7, color='k')
if (idx + i) == 4:
axis.set_ylabel('Player sum')
axis.set_xlabel('Dealer showing')
axis.set_zlim(-1, 1)
axis.set_xlim(1, 10)
axis.set_ylim(12, 21)
axis.set_zticks([-1, 0, 1])
if idx == 1:
axis.text(2, 12, 4, ('U' if u_ace else 'No\nu') + 'sable\nace', fontdict={'ha': 'center'})
axis.set_box_aspect([1,1,0.2])
plt.tight_layout()