When working with computer vision models we frequently need to know information about the camera that was used to generate the image. This includes information about the position of the camera in the world coordinate system as well as the intrinsic properties of the camera such as the focal length. We will write a more detailed post about cameras and coordinate systems later on but for now we will only address the positioning of the camera in the world coordinate system. Think of the world coordinate system as the 3D space in which all the objects in the image live, including the camera.
The position of the camera can be expressed as an R and a T matrix. This can either represent:
- a “world-to-view” transform - this represents the transformation to go from the world coordinate system where the camera lives to the camera position and viewpoint
- a “view-to-world” transform - this represents the inverse transformation to go from the camera viewpoint back to the world coordinate system
Datasets and codebases have different conventions for how cameras are represented. It’s very important to understand the conventions of the codebase and dataset that you are using. For example synthetic data generated using habitat-sim uses the “view-to-world” convention, whereas pytorch3D uses the “world-to-view” convention.
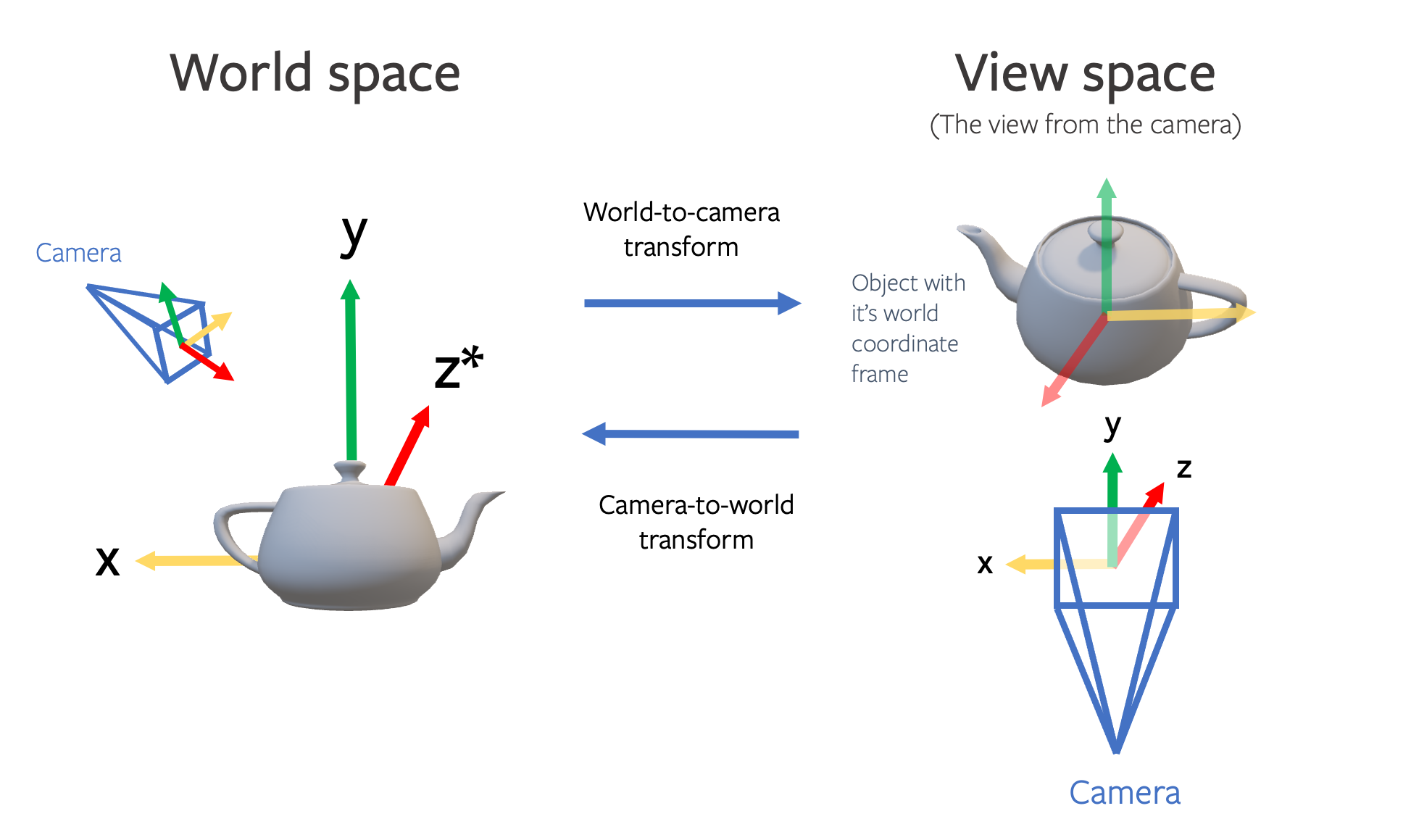
Convention conversion
It’s easy to convert between the two, simply by inverting the 4x4 transformation matrix.
from typing import Tuple
import torch
def convert_cameras(
R: torch.Tensor, T: torch.Tensor
) -> Tuple[torch.Tensor, torch.Tensor]:
"""
Convert camera extrinsics definition from view-to-world to
world-to-view. This requires inverting the 4x4 RT matrix.
Args:
R: torch.FloatTensor of shape (3, 3)
representing the view-to-world transform
T: torch.FloatTensor of shape (1, 3) representing
the camera position in camera coordinates
Returns R, T converted to be a world-to-view transform
"""
assert R.shape == (3, 3)
assert T.shape == (1, 3)
Pinv = torch.eye(4)
# Compose into RT
Pinv[0:3,0:3] = R
Pinv[0:3,3] = T
# Invert
P = torch.linalg.inv(Pinv).to(torch.float32)
# Split back to R and T
R = P[0:3, 0:3]
T = P[0:3, 3]
return R, T
In a later blog post we’ll cover coordinate system conventions in more detail. Understanding the data conventions and the coordinate system in which it lives is extremely important when setting up a deep learning training pipeline.