I have come across an algorithm named furthest point sampling or sometimes farthest point sampling a few times in deep learning papers dealing with point cloud data. However there is a lack of resources online explaining what this algorithm actually does. Here I will try to explain it with reference to this CUDA implementation. Along the way we will also see how to implement it in an efficient parallelised way.
Introduction
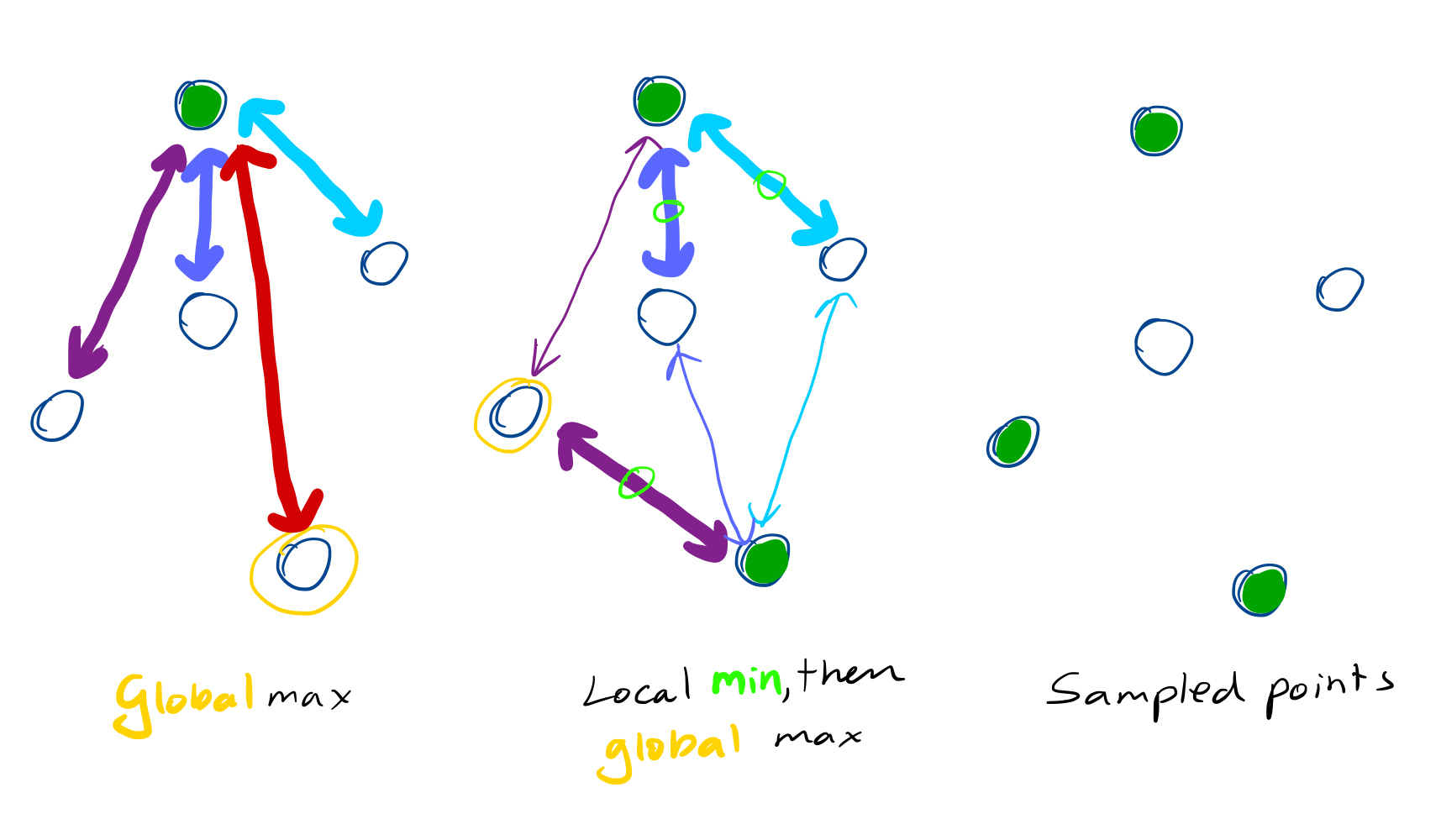
The algorithm is quite simple. You start with a point cloud comprising $N$ points and iteratively select a point until you have up to $S$ samples. You have two sets which we will denote sampled and remaining and you choose a point as follows:
- For each point in
remainingfind its nearest neighbour insampled, saving the distance. - Select the point in
remainingwhose nearest neighbour distance is the largest and move it fromremainingtosampled.
Python
Let us first implement a simple version in Python
def fps(points, n_samples):
"""
points: [N, 3] array containing the whole point cloud
n_samples: samples you want in the sampled point cloud typically << N
"""
points = np.array(points)
# Represent the points by their indices in points
points_left = np.arange(len(points)) # [P]
# Initialise an array for the sampled indices
sample_inds = np.zeros(n_samples, dtype='int') # [S]
# Initialise distances to inf
dists = np.ones_like(points_left) * float('inf') # [P]
# Select a point from points by its index, save it
selected = 0
sample_inds[0] = points_left[selected]
# Delete selected
points_left = np.delete(points_left, selected) # [P - 1]
# Iteratively select points for a maximum of n_samples
for i in range(1, n_samples):
# Find the distance to the last added point in selected
# and all the others
last_added = sample_inds[i-1]
dist_to_last_added_point = (
(points[last_added] - points[points_left])**2).sum(-1) # [P - i]
# If closer, updated distances
dists[points_left] = np.minimum(dist_to_last_added_point,
dists[points_left]) # [P - i]
# We want to pick the one that has the largest nearest neighbour
# distance to the sampled points
selected = np.argmax(dists[points_left])
sample_inds[i] = points_left[selected]
# Update points_left
points_left = np.delete(points_left, selected)
return points[sample_inds]
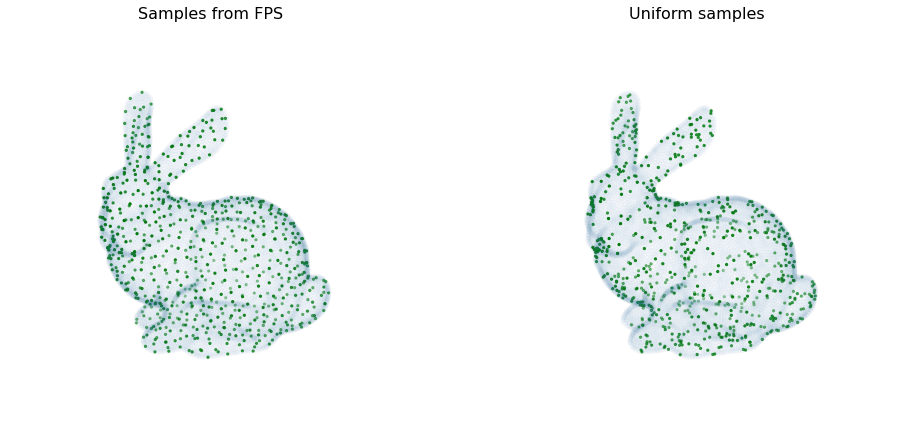
Here we can see it in action. The data used in this figure can be downloaded from here - see the files for Lab 5. We can see that furthest point sampling provides much better coverage of the point cloud compared to uniform sampling.
CUDA
Setting up the kernel
First take a look at the wrapper function
void furthest_point_sampling_kernel_wrapper(int b, int n, int m,
const float *dataset, float *temp,
int *idxs)
We see that the inputs to the kernel are
b - batch_size
n - total points
m - points to sample
data - a $b \times n \times 3$ tensor contain a point-cloud batch
temp - a $b \times n$ tensor filled with 1e10 representing $\infty$
outputs - a $b \times n$ tensor filled with 0
The wrapper makes use of templates to handle cases where you have different block sizes. As we shall see below since the code involves reduction, here finding the max nearest neighbour distance at each iteration and hard-coding the possible block sizes can help to improve performance.
The opt_n_threads function determines block size by choosing the closest power of two that is below the point cloud size work_size.
inline int opt_n_threads(int work_size) {
const int pow_2 = std::log(static_cast<double>(work_size)) / std::log(2.0);
return max(min(1 << pow_2, TOTAL_THREADS), 1);
}
Inside the kernel
Let us now look at what happens in the kernel itself
template <unsigned int block_size>
__global__ void furthest_point_sampling_kernel(
int b, int n, int m, const float *__restrict__ dataset,
float *__restrict__ temp, int *__restrict__ idxs)
-
A kernel specifies what work is done by a single thread
- The data used in the thread is either global (
data,temp,idxs) meaning accessible by all threads in all blocks, shared meaning only threads in the block can access it (distanddist_i) or thread-specific (everything else) distanddist_iare stored in shared memory since for computing the max they will need to be accessed by other threads in the block but not by other blocks [why is this better than global?]
__shared__ float dists[block_size];
__shared__ int dists_i[block_size];
- Threads from other blocks don’t need to access this because this particular kernel assumes that each block handles one batch element here a single point cloud
int batch_index = blockIdx.x;
- The pointer for each of the arrays is advanced to start at the batch element processed by this block.
int batch_index = blockIdx.x;
dataset += batch_index * n * 3;
temp += batch_index * n;
idxs += batch_index * m;
- We will need to refer to the index of the thread often below so grab hold it
int tid = threadIdx.x;
- Whilst each block handles a single batch element, in general we have more points than threads i.e.
n > blocksizeso each thread will process uptoceil(n / block_size)points, stepping through them with astrideofblock_size
const int stride = block_size;
- Before doing anything the first point is chosen and written to global memory
- This is done only by the first thread so before we go ahead we need to call
__syncthreads()to ensure that all threads in the block will subsequently be able to see the update.
Finding the nearest neighbours
- The outer loop is common to all the threads and they all grab the latest sampled point which is
data[blockIdx.x, old]in the point cloud tensor. - We will see what
bestandbestiare used for below.
for (int j = 1; j < m; j++) {
int besti = 0;
float best = -1;
float x1 = dataset[old * 3 + 0];
float y1 = dataset[old * 3 + 1];
float z1 = dataset[old * 3 + 2];
- Each thread however processes different points to compare with
x1, y1, z1. Threads process data in a strided fashion so consecutive threads access consecutive elements at each iteration. This allows coalesced memory access whereby there are fewer accesses to global memory. Very briefly chunks of memory are cached together in cache lines and if access to memory is properly aligned there will be fewer cache lines involved and fewer memory transactions (see these notes for more details)for (int k = tid; k < n; k += stride) -
Within the inner loop this is what happens
-
Select the point which is at
data[blockIndex.x, k]in the point cloud tensor and find the distance to the latest sampled point whose coordinates arex1, y1, z1float x2, y2, z2; x2 = dataset[k * 3 + 0]; y2 = dataset[k * 3 + 1]; z2 = dataset[k * 3 + 2]; -
Skip any points too close to origin
float mag = (x2 * x2) + (y2 * y2) + (z2 * z2); if (mag <= 1e-3) continue; -
Find the distance to the last sampled point
float d = (x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1) + (z2 - z1) * (z2 - z1); -
temp[a]stores the distance between pointaand its nearest neighbour inidx. Since we have just added a point toidxwe need to update this firstfloat d2 = min(d, temp[k]); temp[k] = d2; -
beststores the largest nearest neighbour distance among the points handled by this thread for the present iteration whilstbestistores the index of this point i.e.bestandbestithe local maximum and argmax across the subset points processed by this thread.besti = d2 > best ? k : besti; best = d2 > best ? d2 : best; -
Note that unlike the python code above here the points already in
idxare processed again since using conditionals to skip them would lead to branching that could make the code more inefficient. -
However this is safe since if the iteration after,
ais added toidx,temp[a]will become 0 so it can’t be a max value since all the squared distances are non-negative (unless you had duplicate points* which we will assume is not the case).
-
-
Once the loop is complete write the local maximum and local argmax to shared memory, syncing again
dists[tid] = best; dists_i[tid] = besti; __syncthreads();
Now we have blocksize local maxima and we need to find the furthest point based on these.
Reduction
This is a brief digression about parallelising reduction. This is a complex topic and here I am just mentioning a few points to help you understand this particular implemention. I recommend going through this excellent tutorial if you want to learn more about this topic.
At first glance reduction does not seem possible to parallelise it. For max finding you need to compare elements across the array. A naive version would just use one thread and it would take O(n) time.
A sequential max looks like this:
maxval = -float('inf')
for i in range(N):
if i > tmp:
maxval = i
# Final value of maxval is the result
However in CUDA reduction can be made to run much faster if a divide/conquer approach is adopted as follows:
We assume length of array N is a power of 2. For simplicity, for this example say we have one thread per element so 8 in total:
As an example consider [20, 21, 8, 6, 11, 10, 33, 2] where N=8
- Sequential step 1
-
Split the array into two equal sized parts of length
N/2 = 4[20, 27, 6, 8 | 11, 10, 2, 33] -
Use just half of the thread so 4 threads to compare pairs of elements from each half and store the result in the first part
[20, 27, 6, 33 | 11, 10, 2, 33]
-
- Sequential step 2
-
Now we no longer care about the second part but again divide the first part into two
[20, 27 | 6, 33| -, -, -, -] -
Use just 2 threads now and repeat the comparison
[20, 33 | 6, 33| -, -, -, -]
-
- Sequential step 3
-
Finally we have gotten down to a single pair
[20 | 33 | -, - | -, -, -, -] -
Halving the threads leaves just 1 thread
[33 | 33 | -, - | -, -, -, -] -
Now we have our max
[33 | - | -, - | -, -, -, -]
-
Instead of O(N) iterations we have only O(log(N)), here $\log_2(8) = 3$, sequential steps.
Finding the farthest point
Returning to our code now some further optimisation by using loop unrolling whereby the loop iterations are explicitly written out in advance. This is possible because only a restricted number of block sizes are allowed as we noted before. All the possibilities are hardcoded within the switch block. This means that the if (block_size >= N) statements at compile time resulting in very efficient loop. Refer to this tutorial for more details about these strategies.
All the iterations corresponding to block sizes greater than a given block size will be skipped e.g. if blocksize=256 this will be skipped
if (block_size >= 512) {
if (tid < 256) {
__update(dists, dists_i, tid, tid + 256);
}
__syncthreads();
}
and the thread will start executing from
if (block_size >= 256) {
if (tid < 128) {
__update(dists, dists_i, tid, tid + 128);
}
__syncthreads();
}
As we noted above only threads with 0 <= tid < blocksize/2 will be active with maximum number of active threads halved after each step.
The actual comparison step finds for a pair, the max and based on that the argmax which is what we really care about
__device__ void __update(float *__restrict__ dists, int *__restrict__ dists_i,
int idx1, int idx2) {
const float v1 = dists[idx1], v2 = dists[idx2];
const int i1 = dists_i[idx1], i2 = dists_i[idx2];
dists[idx1] = max(v1, v2);
dists_i[idx1] = v2 > v1 ? i2 : i1;
}
After the last iteration the index of the point with the maximum distance will be found at dists_i[0] and we can add this to the sampled points. Thread 0 updates the global memory accordingly
old = dists_i[0];
if (tid == 0) idxs[j] = old;
And that’s it. You can explores the codebase and read the paper if you want more context and to learn more about using point cloud data in deep learning.
[p1, p2, p3, p4, p5] and p6 = p5. Then you might end up not adding p6 but one of the already present points. Whilst it would not seem to matter even in the cases of duplicate points it might make a difference if the points are non-identical in some other respect e.g. they have some feature that is not considered here.